Fungsi Naik dan Turun
Pertama, kita definisikan suatu fungsi dapat dikatakan sebagai fungsi naik atau fungsi turun. Perhatikan definisi berikut.
Definisi Fungsi Naik dan Turun
Suatu fungsi f dikatakan naik pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) < f(x2).
Suatu fungsi f dikatakan turun pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) > f(x2).
Teorema Uji Fungsi Naik dan Turun
Misalkan f adalah fungsi yang kontinu pada selang tutup [a, b] dan terdiferensialkan pada selang buka (a, b).
- Jika f ’(x) > 0 untuk semua x dalam (a, b), maka f naik pada [a, b].
- Jika f ’(x) < 0 untuk semua x dalam (a, b), maka f turun pada [a, b].
- Jika f ’(x) = 0 untuk semua x dalam (a, b), maka f konstan pada [a, b].
Pembuktian
Kasus 1: Untuk membuktikan kasus pertama, anggap bahwa f ’(x) > 0 untuk semua x dalam selang (a, b) dan misalkan x1 < x2 adalah sembarang dua titik dalam selang tersebut. Berdasarkan Teorema Nilai Rata-Rata, kita tahu bahwa ada suatu bilangan c sedemikian sehingga x1 < c < x2, dan
Karena f ’(c) > 0 dan x2 – x1 > 0, maka f(x2) – f(x1) > 0, yang mengakibatkan bahwa f(x1) < f(x2). Jadi, f naik pada selang tersebut.
Kasus 2: Untuk kasus ini, kita dapat membuktikannya dengan menggunakan alur yang serupa dengan kasus 1.
Kasus 3: Misalkan f ’(x) = 0 untuk semua x dalam selang (a, b) dan misalkan x1 < x2 adalah sembarang duat titik dalam selang tersebut. Berdasarkan Teorema Nilai Rata-Rata, kita tahu bahwa ada suatu bilangan c sedemikian sehingga x1 < c < x2, dan
Karena f ’(c) = 0 maka f(x1) – f(x2) = 0, yang berakibat f(x1) = f(x2). Jadi, fungsi tersebut tidak naik ataupun tidak turun. Dengan kata lain, fungsi tersebut konstan pada selang tersebut.
Teorema Rolle
Teorema Nilai Ekstrim menyatakan bahwa suatu fungsi kontinu pada selang tutup [a, b] harus memiliki nilai minimum dan maksimum pada selang tersebut. Kedua nilai tersebut dapat terjadi pada ujung selang. Teorema Rolle memberikan kondisi yang menjamin keberadaan nilai ekstrim dalam interior suatu selang tertutup.
Teorema RolleMisalkan f kontinu pada selang [a, b] dan terdiferensialkan pada selang buka (a, b). Jika f(a) = f(b), maka terdapat minimal satu bilangan c dalam (a, b) sedemikian sehingga f ’(c) = 0.
Pembuktian Misalkan f(a) = d = f(b).
Kasus 1: Jika f(x) = d untuk semua x dalam [a, b], maka f konstan pada selang tersebut dan f ’(x) = 0 untuk semua x dalam (a, b).
Kasus 2: Misalkan f(x) > d untuk beberapa x dalam (a, b). Berdasarkan Teorema Nilai Ekstrim, kita tahu bahwa f memiliki nilai maksimum pada c dalam selang tersebut. Selanjutnya, karena f(c) > d, nilai maksimum ini tidak terjadi pada kedua ujung selang. Sehingga, f memiliki nilai maksimum dalam selang buka (a, b). Hal ini mengakibatkan f(c) merupakan nilai maksimum lokal dan c merupakan nilai kritis f. Oleh karena itu, karena f terdiferensialkan pada c, kita dapat menarik kesimpulan bahwa f ’(c) = 0.
Kasus 3: Misalkan f(x) < d untuk beberapa x dalam (a, b). Berdasarkan Teorema Nilai Ekstrim, kita tahu bahwa f memiliki nilai minimum pada c dalam selang tersebut. Lebih jauh, karena f(c) < d, nilai minimum tidak terjadi pada kedua ujung selang. Sehingga, f memiliki nilai minimum dalam selang buka (a, b). Hal ini mengakibatkan f(c) merupakan nilai minimum lokal dan c merupakan nilai kritis f. Sehingga, karena f terdiferensialkan pada c, kita dapat menyimpulkan bahwa f ’(c) = 0.
Berdasarkan Teorema Rolle, kita dapat melihat bahwa jika suatu fungsi f kontinu pada [a, b] dan terdiferensialkan pada (a, b), dan jika f(a) = f(b), maka terdapat minimal satu nilai x antara a dan b sedemikian sehingga grafik f memiliki garis singgung horizontal (perhatikan gambar (a) di bawah). Ketika syarat keterdiferensialan tidak dipenuhi dalam Teorema Rolle, f masih memiliki nilai kritis dalam (a, b), tetapi tidak menghasilkan suatu garis singgung horizontal. Seperti yang ditunjukkan oleh gambar (b) di bawah ini.
Contoh 1: Ilustrasi Teorema Rolle
Tentukan dua titik potong terhadap sumbu-x dari fungsi f(x) = x² + 4x + 3 dan tunjukkan bahwa f ’(x) = 0 pada suatu titik di antara kedua titik potong tersebut.
Pembahasan Perhatikan bahwa f terdiferensialkan pada seluruh garis bilangan real. Dengan membuat nol f(x) kita mendapatkan
Sehingga, f(–3) = f(–1) = 0, dan berdasarkan Teorema Rolle kita tahu bahwa ada minimal satu nilai c dalam selang (–3, –1) sedemikian sehingga f ’(c) = 0. Untuk menentukan c tersebut, turunkan f untuk mendapatkan
kemudian selanjutnya kita tentukan f ’(x) = 0 ketika x = –2. Yang perlu diperhatikan adalah bahwa nilai x tersebut terletak dalam selang (–3, –1), seperti yang ditunjukkan gambar di bawah ini.
Teorema Rolle menyatakan bahwa ketika f memenuhi kondisi teorema, maka harus ada minimal satu titik antara a dan b sedemikian sehingga turunannya nol. Tentu saja mungkin ada lebih dari satu titik yang seperti itu, yang dapat diilustrasikan oleh Contoh 2 berikut.
Contoh 2: Ilustrasi Teorema Rolle
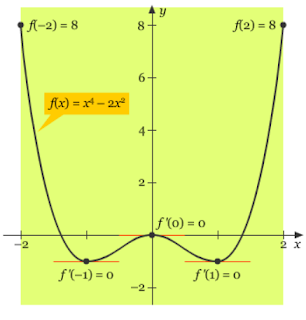
Misalkan f(x) = x4 – 2x². Tentukan semua nilai c pada selang (–2, 2) sedemikian sehingga f ’(c) = 0.
Pembahasan Untuk memulai, perhatikan bahwa fungsi yang diberikan memenuhi kondisi dalam Teorema Rolle, yaitu bahwa f kontinu pada selang [–2, 2] dan terdiferensialkan pada selang (–2, 2). Selanjutnya, karena f(–2) = f(2) = 8, kita dapat menarik kesimpulan bahwa ada minimal satu nilai c dalam (–2, 2) sedemikian sehingga f’(c) = 0. Karena
dengan mengenolkan turunan fungsi tersebut maka dihasilkan
Sehingga, dalam selang (–2, 2), turunan fungsi yang diberikan akan bernilai nol pada tiga tiga nilai yang berbeda, seperti yang ditunjukkan gambar di bawah ini.
No comments:
Post a Comment