Matematika Wajib/Umum Kelas X, XI dan XII : Integral

Pengertian Integral

Integral adalah bentuk operasi matematika yang menjadi invers (kebalikan) dari sebuah operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu.

Berdasarkan pengertian diatas, ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral. Yakni:

Yang Pertama yaitu: Integral sebagai invers atau kebalikan dari turunan yang disebut sebagai Integral Tak Tentu. Yang Kedua yaitu: Integral sebagai limit dari jumlah atau suatu luas daerah tertentu yang disebut Integral Tentu.

Integral Tak Tentu

Integral tak tentu yang seperti sebelumnya dijelaskan adalah merupakan sebuah invers atau kebalikan dari turunan. Yang mana, apabila sebuah turunan dari suatu fungsi, jika diintegralkan akan menghasilkan sebuah fungsi itu sendiri. Contoh perhatikanlah turunan-turunan dalam fungsi aljabar dibawah berikut ini:

Turunan dari fungsi aljabar yakni: y = x³ adalah y’ = 3x²
Turunan dari fungsi aljabar yakni: y = x³ + 8 adalah y’ = 3x²
Turunan dari fungsi aljabar yakni: y = x³ - 6 adalah y’ = 3x²
Turunan dari fungsi aljabar yakni: y = x³ + 17 adalah y’ = 3x²

Didalam sebuah materi turunan, variabel dalam suatu fungsi akan mengalami penurunan pangkat.

Berdasarkan contoh diatas, kita ketahui bahwa ada banyak fungsi yang memiliki hasil turunan yang sama yaitu y’ = 3x². Fungsi dari variabel x³ ataupun fungsi dari variabel x3 yang ditambah atau dikurang suatu bilangan (misal contohnya : +8, +17, atau -6) mempunyai turunan yang sama.

Apabila turunan tersebut dintegralkan, maka seharusnya ialah menjadi fungsi-fungsi awal sebelum diturunkan. Namun, dalam kasus tidak diketahui fungsi awal dari suatu turunan, maka hasil integral dari turunan tersebut dapat dituliskan sebagai berikut:

f(x)= y = x3 + C

Dengan nilai C bisa berapapun jumlahnya. Notasi C ini biasa disebut sebagai konstanta integral.

Integral tak tentu ini dari suatu fungsi dinotasikan sebagai berikut:

$\int f(x) dx$

Pada notasi tersebut, dapat dibaca sebagai integral terhadap notasi x yang disebut integran.

Secara umum integral dari fungsi f(x) ialah penjumlahan F(x) dengan C atau ditulis:

$\int f(x) dx = F(x)$

Oleh karena integral dan turunan saling berkaitan, maka rumus integral dapat diperoleh dari rumusan penurunan tersebut. Maka turunan ialah:

$\frac{d}{dx}\frac{a}{(n+1)}x^{(n+1)} = ax^n$

Maka rumus integral aljabar akan diperoleh:

$\int ax^n dx = \frac{a}{(n+1)}x^{n+1} + C$

dengan syarat-syarat 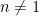$n \neq 1$ .

Sebagai bahan contoh, lihatlah integral aljabar fungsi-fungsi berikut:

$\int 4x^3dx=\frac{4}{(3+1)}x^{(3+1)}+ C = x^4 + C$
$\int \frac{1}{x^3}dx = \int x^{-3} dx = \frac{1}{(-3+1)}x^{-3+1}+C$
$= -\frac{1}{2}x^{-2}+C = -\frac{1}{2x^2}+C$
$\int 4x^3 - 3x^2 dx = \frac{4}{(3+1)} x^{(3+1)} + \frac{3}{(2+1)}x^{(2+1)}+C$
$= x^4+x^3+C$

Integral Tentu

Landasan dasar mengenai integral tentu pertama kali diperkenalkan oleh seorang ilmuan terkenal yaitu Newton dan Leibinz yang kemudian diperkenalkan lebih lanjut secara modern oleh Riemann.

Pengertian Integral ini memiliki batas atas dan batas bawah. Didalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas-batas tertentu atau menghitung volume benda jika diputar.